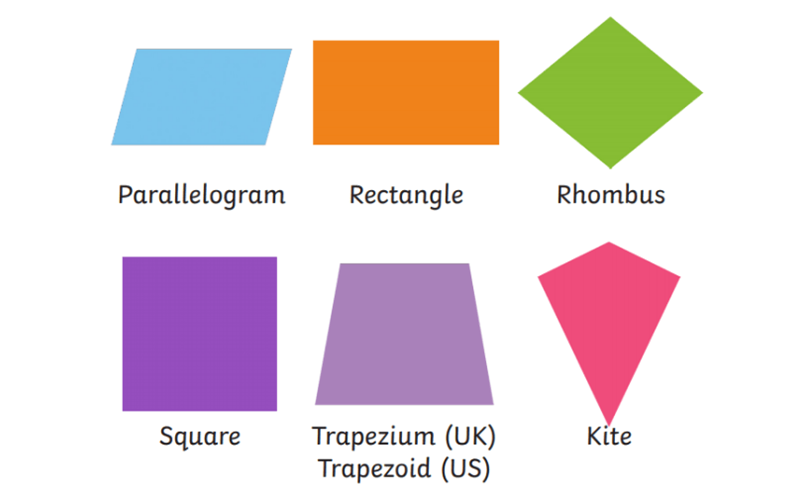
A quadrilateral is any shape that has four points. It has two pairs of parallel sides and two pairs of non-parallel sides. The word “quadrilateral” comes from the Latin word quadri, meaning “four-sided.” Quadrilaterals are an area of geometry that could be difficult to understand, so it’s easier if we explore slowly to find the area of quadrilateral. In geometry, straight-line forms and curved-line forms are two methods to categorize the many different types of forms that exist.
Types of Quadrilaterals
There are 5 types of quadrilaterals on the basis of their shape. These 5 quadrilaterals are:
- Rectangle
- Square
- Parallelogram
- Rhombus / Kite
- Trapezium
Examples of quadrilaterals are Rectangle, Square, Parallelogram, Rhombus, Trapezium, etc., as they all have four vertices and four sides. Square can be said to be the most simple quadrilateral. One thing to note is that the angles inside a quadrilateral measure to a total of 360 degrees. One more kind of quadrilateral known as cyclic quadrilateral is a quadrilateral whose four vertices lie on the circumference or boundary of a circle.
The word area is used in geometry to describe the space encompassed by a given figure. Because our surroundings are densely packed with various forms, it is essential to learn how to calculate the area of the figures that surround us, as in our daily life we come across various geometrical problems like how many bricks would be required to build a wall or how much paint would be required to paint a wall and for this, one needs to know the area of the concerned space.
Area of the different Quadrilaterals
To calculate the area of a quadrilateral, it is very simple. One needs to measure the length of the base, which is the line running through the bottom, and calculate the perpendicular distance of it from the opposite line, which is obtained by drawing a straight line at the right angle to this base. Once the base is multiplied by the height, the area of the quadrilateral is obtained easily. For example, the area of a square is the square of its sides as in a square, the sides already make a right angle. So one side is the base, and the other can be said to be the height. While a rectangle can be said to be an elongated version of the square, its area can be defined as the length multiplied by the breadth, which is again the perpendicular measure taken from the base to the top.
Area of a Rectangle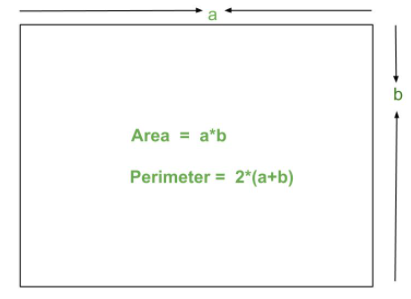
Area of a rectangle = a*b
Where a is Length and b is Width
Area of a Square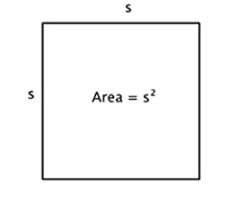
Area of a square = S2
Where S is either side of a square
Area of a Parallelogram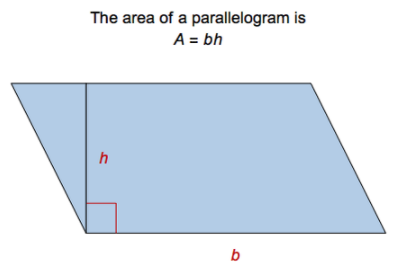
Area of a Parallelogram = b * h
Where b is the baseline and h is the height of the parallelogram.
Area of a Rhombus or Kite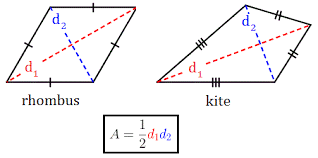
Area of a Rhombus = (d1 * d2) / 2
Where d1 & d2 are the diagonals of the Rhombus or Kite
Area of a Trapezium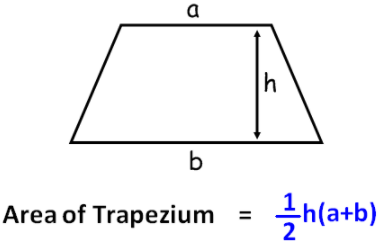
Area of a Trapezium = 1/2 * h(a+b)
Where a and b are the baselines and h is the height of the Trapezium.
Geometry is a discipline of mathematics that, unlike other disciplines of mathematics, employs diagrams or forms for specific topics rather than numbers and notations. Geometry is concerned with a wide range of shapes, and since geometrical shapes are everywhere around us, the study of these shapes holds their own importance in engineering, mechanics, or any other science stream as well. The mathematicians use the area of quadrilateral formula to solve a variety of issues in structures in architecture. Due to their unique features, quadrilaterals are immensely valuable. They are also used in physics to describe distinct force components and to describe vector addition. To lift enormous loads and construct large structures, engineers employ quadrilateral-shaped machines.
Math worksheets may be a useful tool for teaching geometrical principles in a fun way. Students should use this material, which is available on the Cuemath website. The answer keys are also supplied at the back of these worksheets in case students require assistance, and they provide a good explanation of the solution with applicable rationale. Students will obtain the necessary arithmetic skills by practicing with these geometry worksheets on a regular basis, which will improve their problem-solving ability, creative thinking, and arithmetic confidence. Worksheets have problems that are intentionally placed to assist students in understanding ideas while arriving at solutions on their own.
Latest posts by Nirupama Verma (see all)
- What is Corporate Gifting and Why is It Important? - November 8, 2023
- Top 5 Benefits of Synthetic Liquids That You Did Not Know - December 24, 2022
- Pin up Review - September 23, 2022